Polygonal numbers

For a given $k\in\mathbb{Z}^{+},k>2$ , the $k$ -polygonal numbers[1] are a recursively defined integer sequence, as shown in Equation (1).

	$\displaystyle p_{k,1}$	$\displaystyle=1$
	$\displaystyle p_{k,i}$	$\displaystyle=p_{k,i-1}+(k-2)i-(k-3)$		(1)

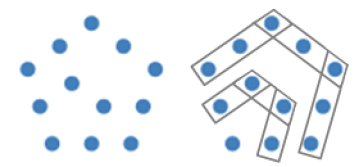
For a term in the sequence $n=p_{k,i}$ , $n$ dots can be arranged in a regular $k$ -polygon built up of $i$ layers (traditionally referred to as gnomons), as shown for the pentagonal numbers ( $k=5$ ) of Figure (1).

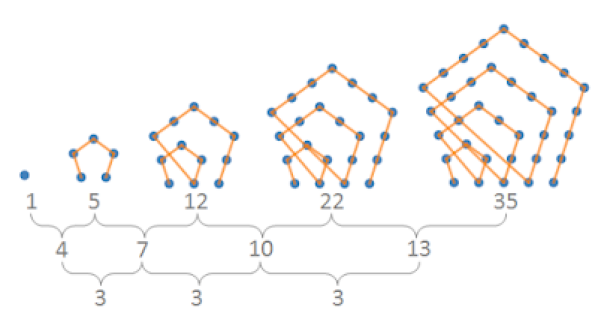
Refer to caption — Figure 1: The first few pentagonal numbers, showing first and second differences

If $n$ is the $i$ th $k$ -polygonal number, it can be drawn as a layered regular $k$ -polygon with $i$ gnomon layers, as shown for the third pentagonal number $12$ , $p_{5,3}=12$ , in Figure (2).