Placing any $n$ in a $k$ -polygonal diagram

Let $n,k\in\mathbb{Z}^{+}$ , $k>2$ . We would like to draw the $k-$ polygonal number diagram “up to” $n$ . If $n$ happens to actually be a $k-$ polygonal number, this will be a complete diagram with $n$ dots in a layered $k$ -polygon. Otherwise, this will be a diagram whose outer gnomon layer is incomplete.

Figure (3) shows hexagonal number ( $k=6$ ) diagrams for the numbers 15 and 26. Because 15 actually is a hexagonal number, the diagram is complete. The diagram for 26 shows an incomplete diagram, with an incomplete outer layer.

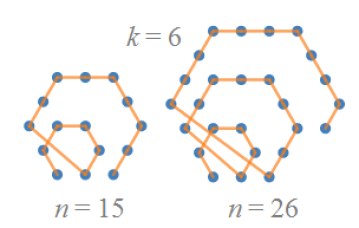
Refer to caption — Figure 3: Two hexagonal diagrams ( $k=6$ ), 15 is hexagonal, 26 is not

Finding the gnomon for $n$ and $k$

The recursive definition for $p_{k,1}$ in Equation (1 yields formulas stated as a summation (2) and a direct calculation (3).

p_{k,i}=\sum^{i}_{j=1}\left[(k-2)j-(k-3)\right]

(2)

p_{k,i}=\frac{(k-2)i(i+1)}{2}-(k-3)i

(3)

Applying the quadratic formula to solve $n-p_{k,i}=0$ provides us with

g\left(n,k\right)=\frac{\left(k-4\right)+\sqrt{\left(k-4\right)^{2}+8n\left(k-% 2\right)}}{2\left(k-2\right)}

(4)

This allows us to identify the gnomon layer $\text{gnomon}(n,k)$ that a given $n$ will sit in within a $k$ -polygonal diagram (5).

\text{gnomon}\left(n,k\right)=\text{ceil}\left(g\left(n\right)\right)

(5)

The position of $n$ within its gnomon layer

The size of the gnomon layer that $n$ will sit in (how many dots would be in the layer within the diagram) is given by Equation (6).

\text{gsize}\left(n,k\right)=1+(\text{gnomon}\left(n,k\right)-1)\cdot\left(k-2\right)

(6)

To find the position of the $n$ th dot within the gnomon, we need to count the number of dots that came before it within that gnomon. To do this we can sum up to $n-1$ over a function whose value is $0$ for all $i$ where $gnomon(i,k)<gnomon(n,k)$ , and whose value is $1$ for those $i$ where $gnomon(i,k)=gnomon(n,k)$ . This sum that gives us the ”depth” of n within its gnomon is provided by Equation (7).

\text{gdepth}\left(n,k\right)=\sum_{i=1}^{n}\left(\text{floor}\left(\frac{% gnomon\left(i,k\right)}{gnomon\left(n,k\right)}\right)\right)

(7)

Placing any nn in a kk-polygonal diagram

Finding the gnomon for nn and kk

The position of nn within its gnomon layer

Placing any $n$ in a $k$ -polygonal diagram

Finding the gnomon for $n$ and $k$

The position of $n$ within its gnomon layer